Exploiting a Biased Coin - Implications for Higher Frequency Trading Strategies

It is said that even the most successful traders are often right only 50-55% of the time.  Yet in markets with scalability, this 55% win rate can yield millions in profits.  The following offers a simplified walk through of why this occurs and ideas to consider for your own betting strategies.  [I used a Jupyter notebook for this simulation - you can get the python code on github here]

First things first: determining a good bet from a bad one
In making a calculated bet, there are two main factors to consider:

1. What is the probability that you are right? 
2. What is the payout (i.e. what are the odds)?

If these two variables yield a positive expectancy, you should take the bet. We'll explore this in more detail with some examples shortly.

In the real world there are different 'shades' of being right, which result in varying profits for winning trades and varying loss amounts for losing trades.  For simplicity though, I restrict the odds to a static number.  You might think of this as the overall average risk/reward expected for a given strategy.

The unbiased coin with even odds
In the case of an unbiased (or fair) coin, we expect the probability of a heads to be .5, or 50%.  We would also expect the odds to be no better than 2-1, meaning for every one dollar we bet, we should expect to get no more than two dollars in return.  Otherwise, odds greater than 2-1 (say even 2.5-1, or 5-2) would imply a favorable trade and we would want to take this bet as frequently as possible with a bet size as large as is reasonable given our account size.


Let's begin
First, let's imagine you flip a coin.  If it lands on heads, you win $100.  If it lands on tails, you lose $100.  The chart below illustrates this idea using a random simulation of 100 coin flips.

Starting with $10,000, as we might expect, we see we end up with what we started with.  However you'll also notice our account fluctuates over the course of these 100 bets. For instance we have a losing stretch that brings our account down near $8800.  How would you feel if you expected to be right half the time but found yourself down $1000? That's the reality of betting even with favorable odds sometimes.  And of course we won't always end up with what we started with even if the odds are 50/50 for each coin flip.  Below I illustrate running this same trial 100 times.

You'll see above that even though we started off with $10,000 in each trial, our ending balance was as low as ~$7500 and as high as ~$12,000.  This is because we can incur stretches of multiple heads (winners) or multiple tails (losers) in a row.  Often they balance out.  Sometimes they don't.  Below we see how often they 'balance out' with a probability distribution of our results illustrated using a histogram.

It is clear from the histogram that while the most probable outcome is that we end up with what we started with, given an unbiased coin with 2-1 (even) odds, there is still a very small chance we end up with a few thousand dollars less or a few thousand more.

The unbiased coin with better odds

It's not very interesting to bet on a coin flip when the probability of heads or tails is 50/50 and when the payout is 2-1.  Note: When you win a 2-1 bet, you get back twice your wager (you bet $50 and you get back $100 ($50 that you bet and $50 in profit)  When you lose a bet, you give up your wager (no matter the odds).  Therefore, flipping coins with these odds is a good way to get nowhere over the long term.  

But what if we increased the payout from 2-1 to 2.5-1 (commonly reported as 5-2).  The same simulation of 100 trials of 100 bets each is shown below, this time with the 'better' odds.

We see that in the 99 of the 100 trials above, we make money or break even, with 'making money' being the most likely outcome.  Here the probability stays the same, but the odds increase and given the combination of these two, this yields positive results. For the sake of comparison, I've included the histogram of these more favorable odds below. 

With better odds, we see our results center roughly around the $12,500 mark as opposed to the $10,000 mark in the first example.  This is a nice improvement in results with only a relatively small change in our odds.

What about a biased coin?

Up until now, we've looked at unbiased coins with an equal probability of winning and losing, that is 50% chance of both heads and tails.  What if we now change the probability?  How does that improve or hurt our expected returns?

 75% probability of "winning" each coin flip

 60% probability of "winning" each coin flip

40% probability of "winning" each coin flip

The three charts above show coins each with a different bias.  As expected coins with a favorable bias (above 50%) result in overwhelming positive results and vice versa.  Note however in the third chart that we only have a 40% chance of being right on each coin flip yet there is one example of us ending up with ~$11,000.

Putting it all together

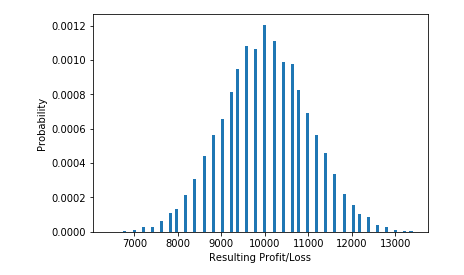
In the real world, both the probabilities and payouts are not so clean.  Still, different trading strategies do cluster around similar win rates and payouts. For example, a high frequency strategy may have a near even money payout (say 2.25-1) and only 45% win rate yet still be very profitable assuming a) it could scale and b) frictional costs do not negate the expectancy.  That simulation is shown below.

Even though we are wrong more than we are right, the payout (2.25-1) in this case make up for this and we see a very successful trading strategy (again, ignoring frictional costs).

So how do you figure out the minimum payout needed to be profitable for a given trading strategy? To get a basic model for any strategy, you only need the win-rate and payout.  To find the win rate, you might run a historical test to get a rough estimate.  With that you can do some simple math to figure out your minimum break even odds for this strategy.

winRate * payout = 1

payout = 1 / winRate

= 1 / 0.45

= 2.2222

So for a strategy that is right 45 times out of 100, it can still be profitable as long as the payout is greater than 2.2222 to 1.  Our last model above confirms this with a 2.5 to 1 payout.

Below I created a graphic in Tableau to show the minimum payout (odds) needed for strategies with a given win rate.  Using our previous example, you can verify that a strategy with a win rate of 45% needs at least 2.22 to 1 odds to be profitable.

A final example

To get a taste of what this all means in the real world, let's imagine you work at a quant fund.  You have been given $1,000,000 in trading capital.  You decide to risk 1% of capital per trade ($10,000).  You have a strategy that finds on average 10,000 trades per month.  You are right only 45% of the time and get odds of 2.5-1 per trade.  How much profit do you make, each month? (think of an answer then highlight the white space below to see the result of my simulation)

$12 million per month

Drop that 45% win-rate down to 40% though and you made only $1,500 in a month.  After fees, you would almost certainly be in the red.  These simulations show that even small variations in the win-rate or payout can result in vastly different outcomes. 

As they say in football, "it's a game of inches".

Good luck out there.



Topics for further exploration 

• Seasonal strategies - alternating viability of strategies throughout the year or through various stages of economic cycles
• Add trade frequency feature to this model creating a more complete, 3-D view of strategy viability

Authors note: Until now, my trading style has not relied on making tens of thousands of trades per year.  However with the significant declines in volatility over the last several years, I am adapting. My previous style involved taking trades with skewed risk/reward odds of at least 3-1 and a probability of being right as low as 40% though typically higher.  As was shown above, this proves to be a profitable approach yielding very small draw downs over the long term.  It further proves worthwhile when trade frequency exceeds a certain threshold.